Causal Representation Learning

List of publications

Tutorials: At AAAI 2025 slides and NASIT 2025 slides video-part1 video-part2
Score-based Causal Representation Learning: Linear and General Transformations (JMLR): considers single-node interventions for linear and general transformations
ROPES: Robotic Pose Estimation via Score-based Causal Representation Learning (NeurIPS’25 Workshop): an application on robotic pose estimation
General Identifiability and Achievability for Causal Representation Learning (AISTATS’24): considers general transformations with single-node interventions (JMLR paper significantly extends this preliminary version)
Linear Causal Representation Learning from Unknown Multi-node Interventions (NeurIPS’24): multi-node interventions on Linear CRL
Sample Complexity of Interventional Causal Representation Learning (NeurIPS’24): sample-complexity analysis of linear CRL
Score-based causal representation learning with interventions: very first paper which establishes the foundations of score-based CRL idea, for non-linear latent causal models and linear transforms.

See below for a conceptual summary of this line of work, settings and key results of the papers mentioned above.

Project summary:

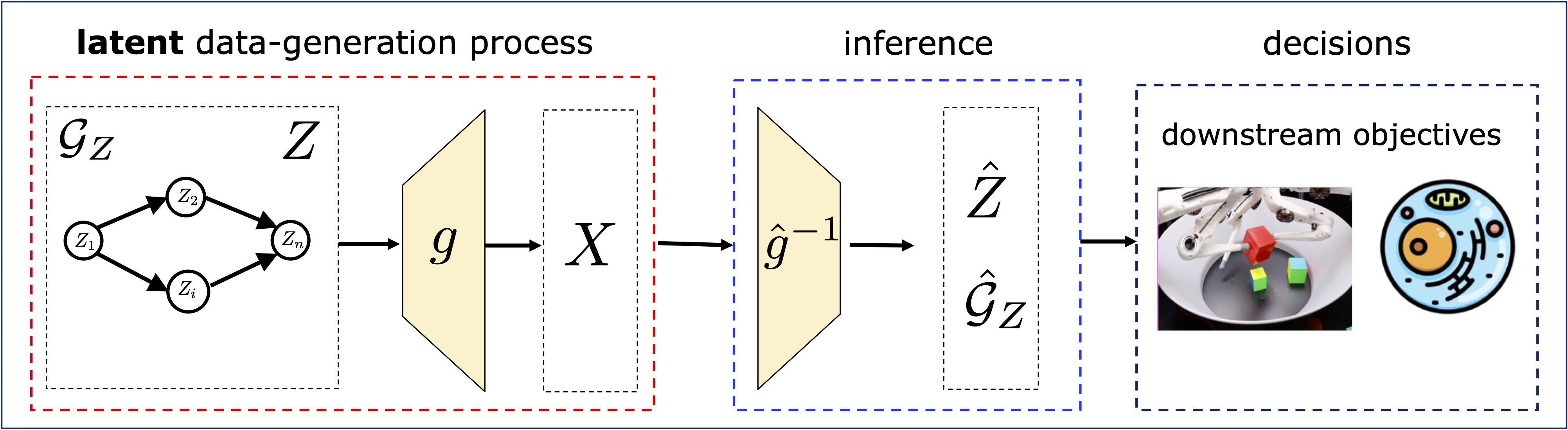
In causal representation learning (CRL), we consider a data-generating process in which the high-dimensional observations $X$ are generated from low-dimensional, causally-related variables $Z$ through an unknown transformation $g$ as $X=g(Z)$. The causal relationships among the latent variables are captured by a directed acyclic graph (DAG) ${\cal{G}}_{Z}$ over $Z$.

The central goal of CRL is to use the observed data $X$ to recover $Z$ and ${\cal{G}}$. This process is typically facilitated by learning an inverse of the data-generating process, i.e., $g^{-1}$ as the inverse of the unknown generative mapping $g$. We focus on two central questions:

Identifiability: Determining the necessary and sufficient conditions under which ${\cal{G}}$ and $Z$ can be recovered. This is known to be impossible without additional supervision or sufficient statistical diversity among the samples of the observed data $X$ (a simple example is that Gaussians are rotation-invariant, making it difficult to identify them under a linear mapping). Thus, the scope of identifiability (e.g., node-level, perfect, partial etc.) critically depends on the extent of information available about the data and the underlying data-generation process.

Achievability: is the notion of designing tractable algorithms that can recover $Z$ and $\mathcal{G}$, while maintaining identifiability guarantees. Note that identifiability results can be non-constructive, without specifying feasible algorithms. Hence, we make the distinction and aim to design practical algorithms for achieving constructive identifiability results.

To ensure identifiability along with tractable algorithms, we need to look for a reasonable combination of (i) assumptions on the data-generation (model class we consider), and (ii) richer observations.

Interventions / Multi-environments as Diverse Data Sources

Consider observing data from multiple related environments. Typically, differences between those environments can be explained by changes in a few key factors. In other words, taking the view that high-dimensional data lie in a low-dimensional manifold, sparse changes in the low-dimensional representation can explain the differences across environments. From CRL viewpoint, these sparse changes can be formalized by interventions on the latent causal space, which provide the sufficient richer observations to enable identifiability of latent variables and graph. Specifically, in addition to observational environment, we consider a set of given interventional environments, in which a subset of nodes are intervened in each. In this framework, we only use distribution level information, meaning that we use the interventions as a weak form of supervision via having access to only the pair of distributions before and after an intervention (as opposed to requiring pairs of observed and intervened samples). This allows us:

model distribution shifts via changes in causal mechanisms
contrast interventional vs. observational distributions
if changes are sparse, gives a natural way to restrain the solution set

To harness the additional knowledge induced by the interventions, we developed score-based CRL. The key idea is that latent score functions (gradients of log-densities) encode intervention effects as sparse variations across environments. By linking score functions of observed data (which can be efficiently estimated even in high-dimensional settings) to latent scores, we obtain tractable learning objectives and algorithms. In short, we develop algorithms that search for representations whose inter-environment differences are maximally sparse, aligning them with the true causal mechanisms.

The theoretical foundations of CRL have two main axes: (i) model complexity, i.e., how expressive the true causal mechanisms and the mapping from latent to observed data are; and (ii) data richness, i.e., what diversity of environments and interventions is necessary and sufficient for identifiability. This perspective clarifies which structural assumptions and data resources are needed in different regimes.

Ideally, one would prefer no restriction on intervention size, type, or knowledge. In our work, we consider a spectrum of settings to lay out the identifiability landscape and accompanying algorithms, e.g., linear vs. general transformations, single-node vs. multi-node interventions, soft vs. hard interventions. Before

Score-based CRL

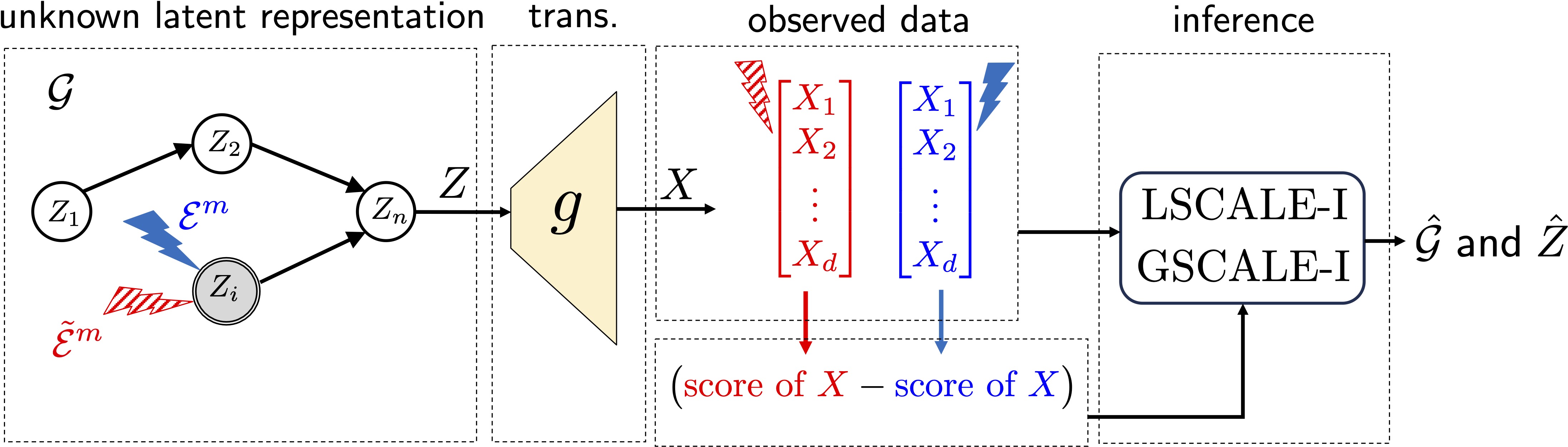
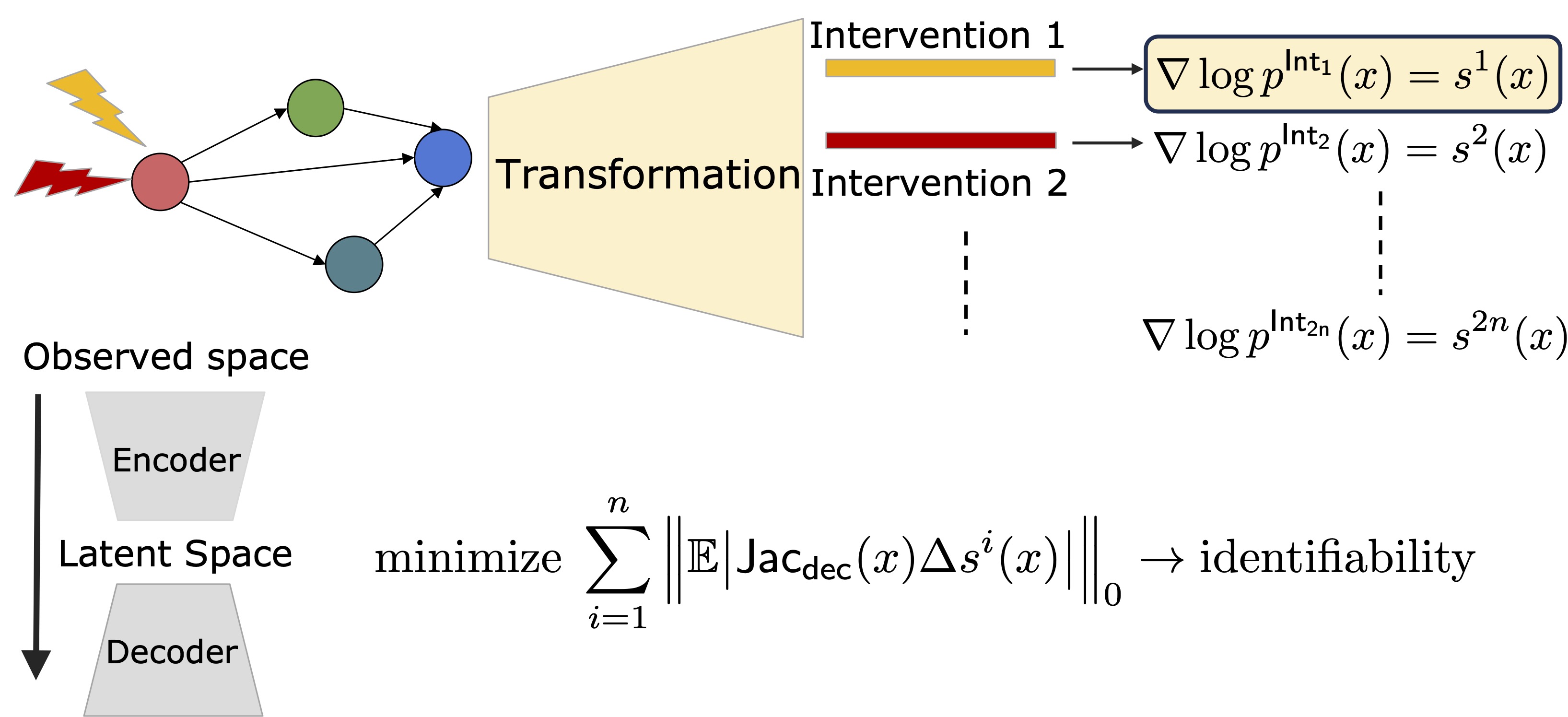
In our papers, we establish the connections between score functions (gradient of the log-density) and interventional distributions. Specifically, we show that differences in score functions across different environment pairs contain all the information about the latent DAG. Leveraging this property, we show that the data-generating process can be inverted by finding the inverse transform that minimizes the score differences in the latent space. Using this approach, we develop constructive proofs of identifiability and algorithms in various settings. To give an insight, there are two key properties of score functions that make this idea work. Denote $s(z) = \nabla \log_z p(z)$ and $s_X(x) = \nabla \log_x p(x)$ for observational distributions $p(z)$ and $p_X(x)$. Use superscript $^m$ to denote corresponding definitions in interventional environment ${\cal E}^m$.

Score differences are sparse: Consider a single-node intervention, e.g., node $i$ is intervened in ${\cal E}^m$. Then, the score difference function $s(z) - s^m(z)$ will be sparse, with indices of non-zero entries exactly correspond to the parents of the intervened node. This implies that given access to all single-node interventions, changes in the score functions exactly give DAG structure!

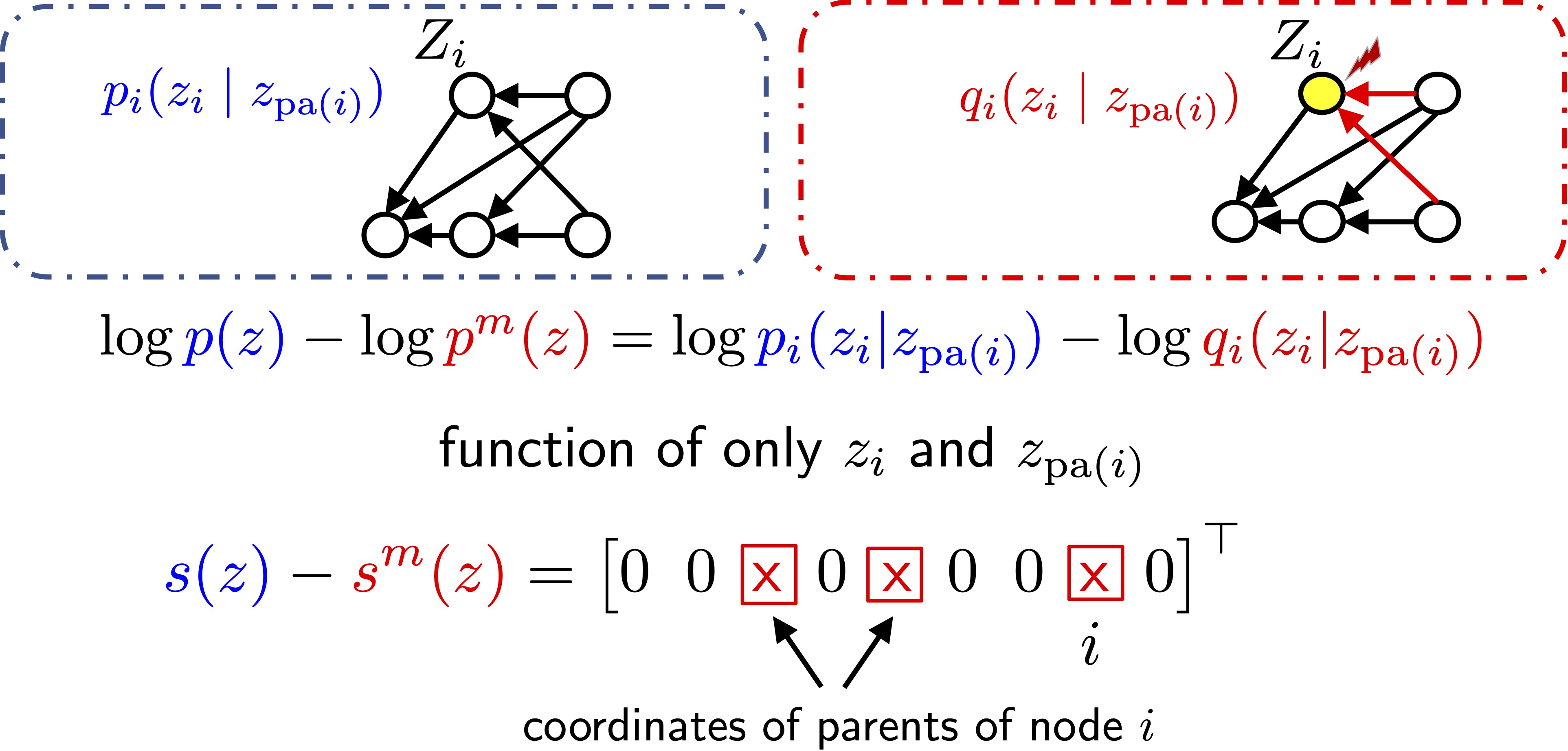
How can we use this property to guide our learning of an inverse transform? Consider a candidate encoder $h$, and \let $\hat{Z} = h(X)$. Intuitively, we can use the sparsity of the true latent score differences to find the true encoder $g^{-1}$, i.e., the estimated latent score differences cannot be sparser than the true score differences.

Latent score differences can be computed from observed score differences: So far, the nice sparsity properties of score functions above are for latent variables, since these properties stem from the causal relationships and interventions on the latents. However, we have only access to observed $X$ variables. In terms of pure identifiability objective, one can suggest computing the score functions of $\hat{Z}$ for every possible encoder $h$, which is infeasible. Instead, we take a constructive approach and show that latent score differences can be computed from observed score differences using the Jacobian of $h^{-1}$. Specifically, $s_{\hat{Z}} ({\hat{z}}) - s_{\hat{Z}}^{m}({\hat{z}}) = J_{h^{-1}}({\hat{z}})^{\top} (s_{X} (x) - s_{X}^{m}(x))$.

How to form an objective function?: Different settings (i.e., a pair data-generation model and observed data) require different levels of algorithm design (e.g., dealing with multi-node interventions, parametric vs. nonparametric construction etc.). At their cores though, those different methods rely on the same principle of algorithmically enforcing the sparse changes on the latent mechanisms. Using the link between score functions of observed and latent variables, this principle can be summarized as learning an (encoder,decoder) pair $(f,h)$ that (i) minimizes score variations in the latents across environments, and (ii) ensures perfect reconstruction:

\[\mathcal{L}(h, f) = \underbrace{\mathbb{E}\!\left[\| f \circ h(x) - x \|^2\right]}_{\text{Reconstruction Loss}} + \lambda \underbrace{\left\| \mathbb{E}\!\left[ \textrm{Jac.}_f(\hat{z})^{\top} \cdot \left(\Delta s_X(x)\right) \right] - e_i \right\|^2}_{\text{Sparsity Loss}}.\]

Score-based Causal Representation Learning: Linear and General Transformations (JMLR’25)

Paper Code

TLDR:

Linear transform, general causal models, one single-node intervention per node.
Hard interventions: element-wise identifiability up to scaling and perfect recovery of DAG.
Soft interventions: identifiability up to parents. If the causal model is sufficiently nonlinear, then latent DAG is fully identified and latent variables are identified up to surrounding variables (shown to be a tight result)
General transform: reorganization of the AISTATS paper, with additional experiments.

ROPES: Robotic Pose Estimation via Score-based Causal Representation Learning (NeurIPS’25 EMW Workshop)

Paper

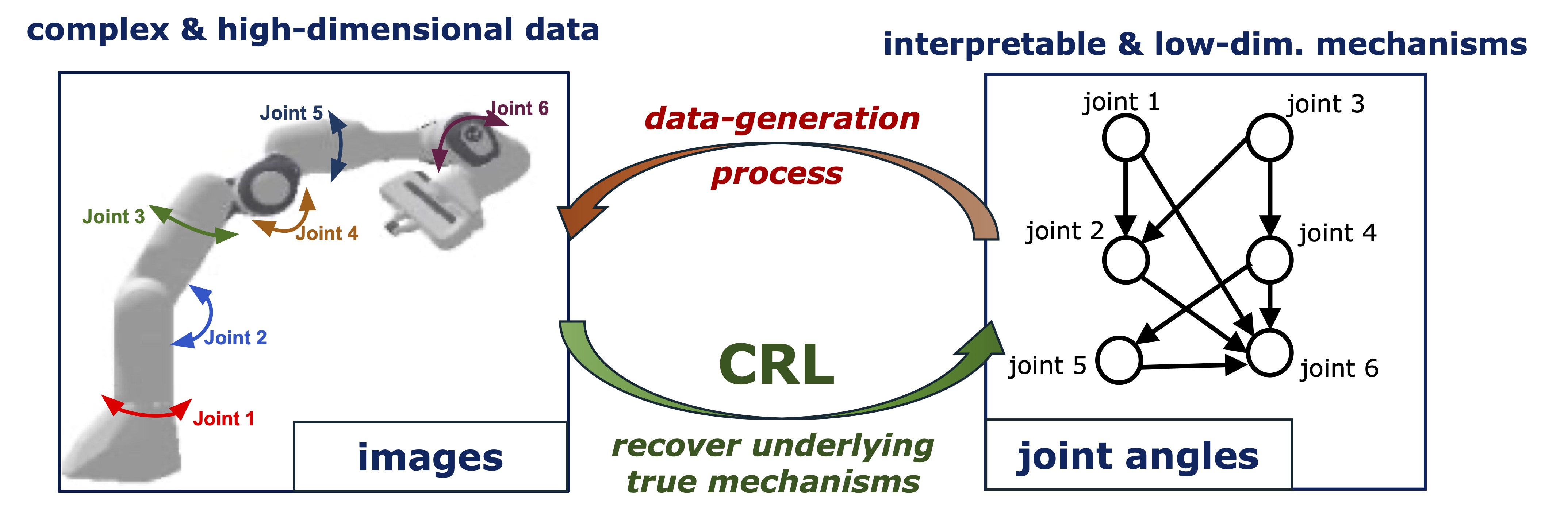
TLDR: Taking a step towards bridging the theory-practice gap in interventional CRL by applying it to robot pose estimation problem.

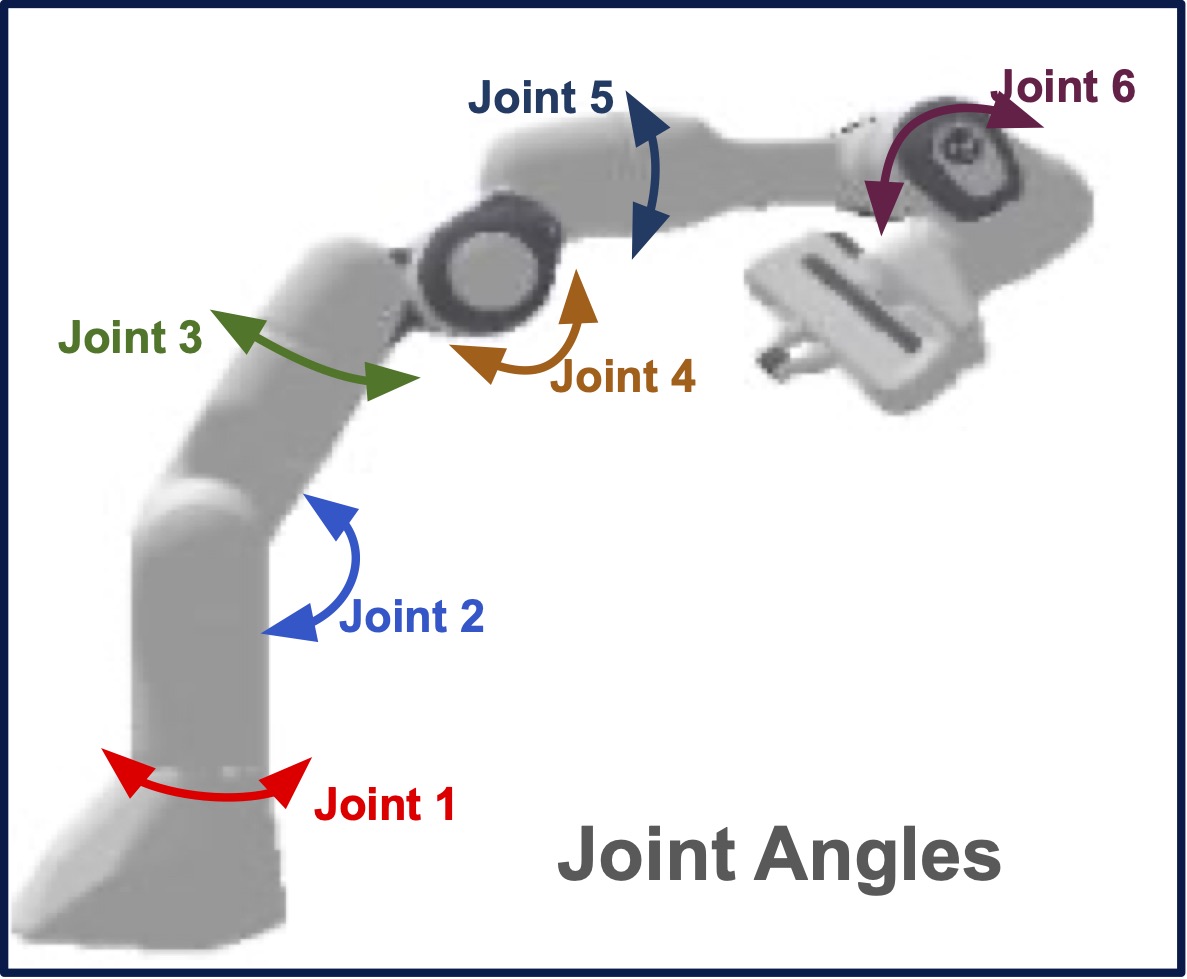
Formalization: Pose estimation as a CRL problem in which robot joint angles are treated as controllable latent causal variables embedded in a larger generative mapping
Methodology: ROPES, an autoencoder-based architecture augmented with interventional regularizers that rely on score variations upon interventions. This relies on score-based CRL algorithms.
Empirical validation: Use common simulators with multi-joint robot and collect visual data. Showing a strong correlation between the angles recovered by ROPES and the ground truth values, verifying successful disentanglement
No reliance on pose labels: Showing disentanglement by exploiting distributional changes and therefore requires no conventional supervision from pose labels.
Comparison with state-of-the-art: ROPES, without using labels except a final calibration step, achieves comparable performance to state-of-the-art RoboPEPP, which uses a JEPA-based self-supervised backbone followed by supervised training to predict joint angles. Specifically, our ablation study shows that RoboPEPP requires a substantial amount of labeled data to outperform our pose-label-free CRL-based method.

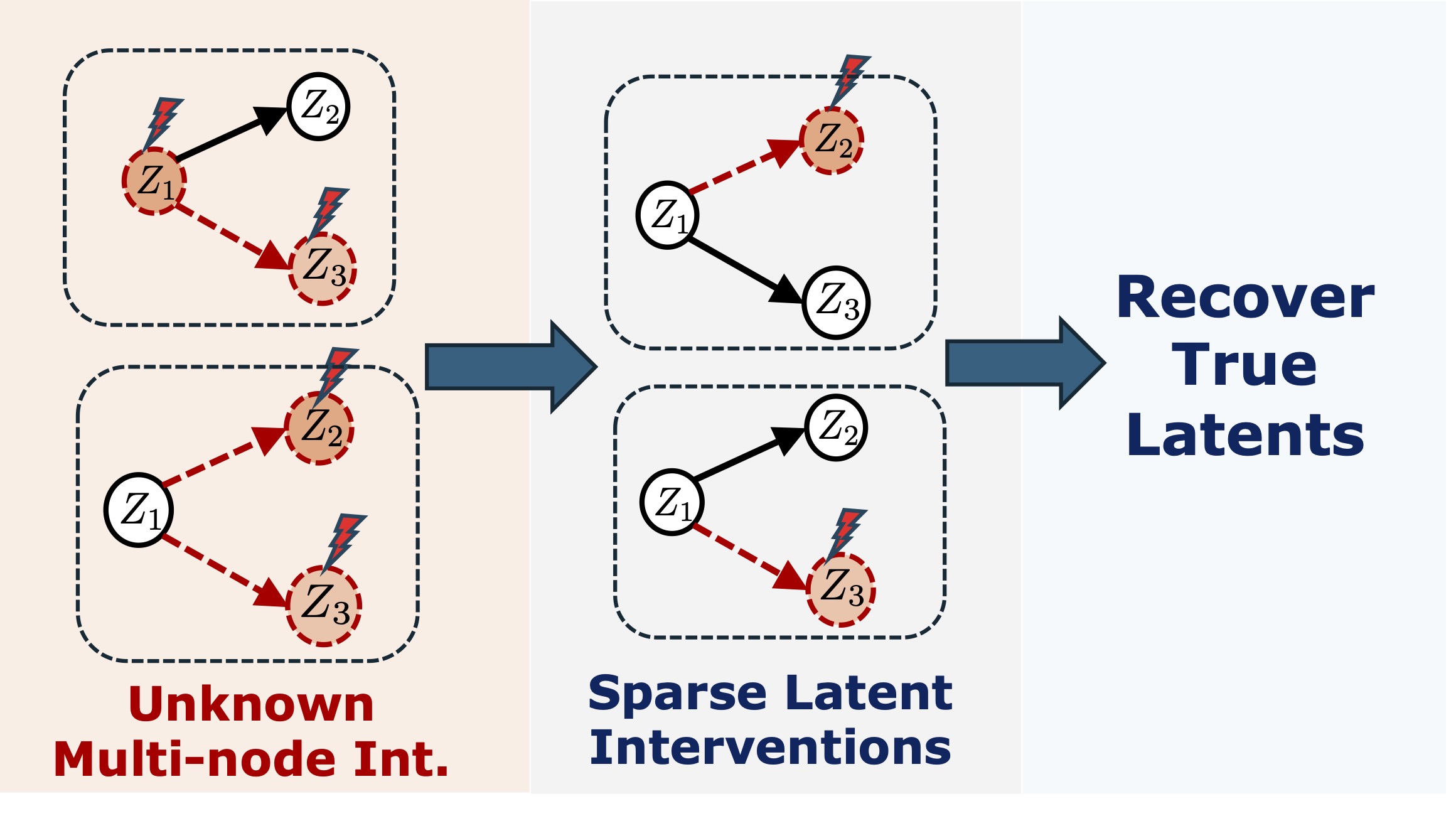
Linear Causal Representation Learning from Unknown Multi-node Interventions (NeurIPS’24)

Paper Code Poster

TLDR:

Linear transform, general causal models, unknown multi-node interventions. Same guarantees as single-node interventions!
Hard interventions: element-wise identifiability up to scaling and perfect recovery of DAG.
Soft interventions: identifiability up to ancestors
Requirement: multi-node interventions are diverse enough, specified as having a full-rank intervention signature matrix.

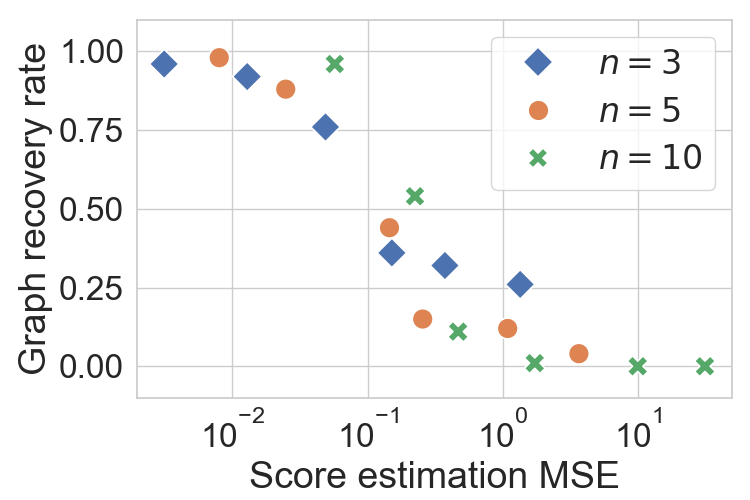
Sample Complexity of Interventional Causal Representation Learning (NeurIPS’24)

Paper Poster

TLDR:

Linear transform, general causal models, one single-node soft intervention per node.
First sample complexity results for interventional CRL!
Probably approximately correct (PAC)-identifiability via generic score estimators.
Specific sample complexity results for an RKHS-based score estimator.

General Identifiability and Achievability for Causal Representation Learning (AISTATS’24 oral)

Paper Code Talk Poster

TLDR:

General transform, general causal models, two single-node hard interventions per node suffice for element-wise identifiability (up to an intervible transform)!
First provably correct algorithm for general transforms! Experiments with images confirm the scalability.
Benefits: do not require faithfulness assumption of causal discovery, and do not require to know which pair of environments intervene on the same node.

References

2025

JMLR
Score-based causal representation learning: Linear and General Transformations

Burak Varıcı*, Emre Acartürk*, Karthikeyan Shanmugam, Abhishek Kumar, and Ali Tajer

Journal of Machine Learning Research, 2025

Abs Bib PDF Code

This paper addresses intervention-based causal representation learning (CRL) under a general nonparametric latent causal model and an unknown transformation that maps the latent variables to the observed variables. Linear and general transformations are investigated. The paper addresses both the identifiability and achievability aspects. Identifiability refers to determining algorithm-agnostic conditions that ensure recovering the true latent causal variables and the latent causal graph underlying them. Achievability refers to the algorithmic aspects and addresses designing algorithms that achieve identifiability guarantees. By drawing novel connections between score functions (i.e., the gradients of the logarithm of density functions) and CRL, this paper designs a score-based class of algorithms that ensures both identifiability and achievability. First, the paper focuses on linear transformations and shows that one stochastic hard intervention per node suffices to guarantee identifiability. It also provides partial identifiability guarantees for soft interventions, including identifiability up to ancestors for general causal models and perfect latent graph recovery for sufficiently non-linear causal models. Secondly, it focuses on general transformations and shows that two stochastic hard interventions per node suffice for identifiability. Notably, one does not need to know which pair of interventional environments have the same node intervened. Finally, the theoretical results are empirically validated via experiments on structured synthetic data and image data.
@article{varici2025score, title = {Score-based causal representation learning: Linear and General Transformations}, author = {Var{\i}c{\i}*, Burak and Acart{\"u}rk*, Emre and Shanmugam, Karthikeyan and Kumar, Abhishek and Tajer, Ali}, journal = {Journal of Machine Learning Research}, year = {2025}, volume = {26}, number = {112}, pages = {1--90}, rank = {1} }
NeurIPS Workshop
ROPES: Robotic Pose Estimation via Score-based Causal Representation Learning

Pranamya Prashant Kulkarni, Puranjay Datta, Burak Varıcı, Emre Acartürk, Karthikeyan Shanmugam, and Ali Tajer

arXiv:2510.20884, (NeurIPS 2025 Workshop on Embodied World Models for Decision Making), 2025

Abs Bib PDF

Causal representation learning (CRL) has emerged as a powerful unsupervised framework that (i) disentangles the latent generative factors underlying high-dimensional data, and (ii) learns the cause-and-effect interactions among the disentangled variables. Despite extensive recent advances in identifiability and some practical progress, a substantial gap remains between theory and real-world practice. This paper takes a step toward closing that gap by bringing CRL to robotics, a domain that has motivated CRL. Specifically, this paper addresses the well-defined robot pose estimation – the recovery of position and orientation from raw images – by introducing Robotic Pose Estimation via Score-Based CRL (ROPES). Being an unsupervised framework, ROPES embodies the essence of interventional CRL by identifying those generative factors that are actuated: images are generated by intrinsic and extrinsic latent factors (e.g., joint angles, arm/limb geometry, lighting, background, and camera configuration) and the objective is to disentangle and recover the controllable latent variables, i.e., those that can be directly manipulated (intervened upon) through actuation. Interventional CRL theory shows that variables that undergo variations via interventions can be identified. In robotics, such interventions arise naturally by commanding actuators of various joints and recording images under varied controls. Empirical evaluations in semi-synthetic manipulator experiments demonstrate that ROPES successfully disentangles latent generative factors with high fidelity with respect to the ground truth. Crucially, this is achieved by leveraging only distributional changes, without using any labeled data. The paper also includes a comparison with a baseline based on a recently proposed semi-supervised framework. This paper concludes by positioning robot pose estimation as a near-practical testbed for CRL.
@article{kulkarni2025ropes, title = {{ROPES}: Robotic Pose Estimation via Score-based Causal Representation Learning}, author = {Kulkarni, Pranamya Prashant and Datta, Puranjay and Var{\i}c{\i}, Burak and Acart{\"u}rk, Emre and Shanmugam, Karthikeyan and Tajer, Ali}, journal = {arXiv:2510.20884, (NeurIPS 2025 Workshop on Embodied World Models for Decision Making)}, year = {2025}, }

2024

NeurIPS
Linear Causal Representation Learning from Unknown Multi-node Interventions

Burak Varıcı, Emre Acartürk, Karthikeyan Shanmugam, and Ali Tajer

In Proc. Advances in Neural Information Processing Systems, 2024

Abs Bib PDF Code Poster Slides

Despite the multifaceted recent advances in interventional causal representation learning (CRL), they primarily focus on the stylized assumption of single-node interventions. This assumption is not valid in a wide range of applications, and generally, the subset of nodes intervened in an interventional environment is fully unknown. This paper focuses on interventional CRL under unknown multi-node (UMN) interventional environments and establishes the first identifiability results for general latent causal models (parametric or nonparametric) under stochastic interventions (soft or hard) and linear transformation from the latent to observed space. Specifically, it is established that given sufficiently diverse interventional environments, (i) identifiability up to ancestors is possible using only soft interventions, and (ii) perfect identifiability is possible using hard interventions. Remarkably, these guarantees match the best-known results for more restrictive single-node interventions. Furthermore, CRL algorithms are also provided that achieve the identifiability guarantees. A central step in designing these algorithms is establishing the relationships between UMN interventional CRL and score functions associated with the statistical models of different interventional environments. Establishing these relationships also serves as constructive proof of the identifiability guarantees.
@inproceedings{varici2024linear, title = {Linear Causal Representation Learning from Unknown Multi-node Interventions}, author = {Var{\i}c{\i}, Burak and Acart{\"u}rk, Emre and Shanmugam, Karthikeyan and Tajer, Ali}, booktitle = {Proc. Advances in Neural Information Processing Systems}, year = {2024}, video_short = {https://neurips.cc/virtual/2024/poster/93136}, }
NeurIPS
Sample Complexity of Interventional Causal Representation Learning

Emre Acartürk, Burak Varıcı, Karthikeyan Shanmugam, and Ali Tajer

In Proc. Advances in Neural Information Processing Systems, 2024

Abs Bib PDF Poster

Consider a data-generation process that transforms low-dimensional latent causally-related variables to high-dimensional observed variables. Causal representation learning (CRL) is the process of using the observed data to recover the latent causal variables and the causal structure among them. Despite the multitude of identifiability results under various interventional CRL settings, the existing guarantees apply exclusively to the infinite-sample regime (i.e., infinite observed samples). This paper establishes the first sample-complexity analysis for the finite-sample regime, in which the interactions between the number of observed samples and probabilistic guarantees on recovering the latent variables and structure are established. This paper focuses on general latent causal models, stochastic soft interventions, and a linear transformation from the latent to the observation space. The identifiability results ensure graph recovery up to ancestors and latent variables recovery up to mixing with parent variables. Specifically, $O((\log \frac{1}δ)^4)$samples suffice for latent graph recovery up to ancestors with probability $1 - δ$, and $\cal O((\frac{1}{ε}\log \frac1δ)^4)$samples suffice for latent causal variables recovery that is $ε$close to the identifiability class with probability $1 - δ$.
@inproceedings{acarturk2024sample, title = {Sample Complexity of Interventional Causal Representation Learning}, author = {Acart{\"u}rk, Emre and Var{\i}c{\i}, Burak and Shanmugam, Karthikeyan and Tajer, Ali}, booktitle = {Proc. Advances in Neural Information Processing Systems}, year = {2024}, }
AISTATS (oral)
General Identifiability and Achievability for Causal Representation Learning

Burak Varıcı, Emre Acartürk, Karthikeyan Shanmugam, and Ali Tajer

In Proc. International Conference on Artificial Intelligence and Statistics, 2024

Abs Bib PDF Code Poster Slides

This paper focuses on causal representation learning (CRL) under a general nonparametric latent causal model and a general transformation model that maps the latent data to the observational data. It establishes identifiability and achievability results using two hard uncoupled interventions per node in the latent causal graph. Notably, one does not know which pair of intervention environments have the same node intervened (hence, uncoupled). For identifiability, the paper establishes that perfect recovery of the latent causal model and variables is guaranteed under uncoupled interventions. For achievability, an algorithm is designed that uses observational and interventional data and recovers the latent causal model and variables with provable guarantees. This algorithm leverages score variations across different environments to estimate the inverse of the transformer and, subsequently, the latent variables. The analysis, additionally, recovers the identifiability result for two hard coupled interventions, that is when metadata about the pair of environments that have the same node intervened is known. This paper also shows that when observational data is available, additional faithfulness assumptions that are adopted by the existing literature are unnecessary.
@inproceedings{varici2024general, title = {General Identifiability and Achievability for Causal Representation Learning}, author = {Var{\i}c{\i}, Burak and Acart{\"u}rk, Emre and Shanmugam, Karthikeyan and Tajer, Ali}, booktitle = {Proc. International Conference on Artificial Intelligence and Statistics}, year = {2024}, address = {Valencia, Spain}, rank = {5} }

2023

arXiv
Score-based causal representation learning with interventions

Burak Varıcı, Emre Acartürk, Karthikeyan Shanmugam, Abhishek Kumar, and Ali Tajer

arXiv:2301.08230, 2023

Abs Bib PDF Slides

This paper studies the causal representation learning problem when the latent causal variables are observed indirectly through an unknown linear transformation. The objectives are: (i) recovering the unknown linear transformation (up to scaling) and (ii) determining the directed acyclic graph (DAG) underlying the latent variables. Sufficient conditions for DAG recovery are established, and it is shown that a large class of non-linear models in the latent space (e.g., causal mechanisms parameterized by two-layer neural networks) satisfy these conditions. These sufficient conditions ensure that the effect of an intervention can be detected correctly from changes in the score. Capitalizing on this property, recovering a valid transformation is facilitated by the following key property: any valid transformation renders latent variables’ score function to necessarily have the minimal variations across different interventional environments. This property is leveraged for perfect recovery of the latent DAG structure using only soft interventions. For the special case of stochastic hard interventions, with an additional hypothesis testing step, one can also uniquely recover the linear transformation up to scaling and a valid causal ordering.
@article{varici2023score, title = {Score-based causal representation learning with interventions}, author = {Var{\i}c{\i}, Burak and Acartürk, Emre and Shanmugam, Karthikeyan and Kumar, Abhishek and Tajer, Ali}, journal = {arXiv:2301.08230}, year = {2023}, }